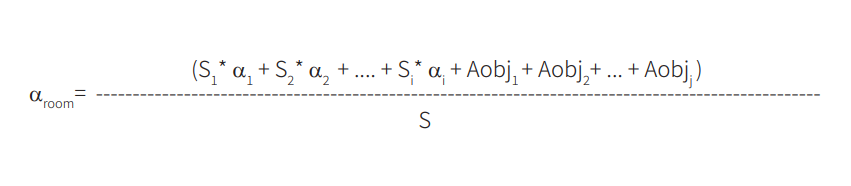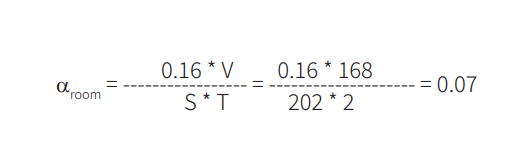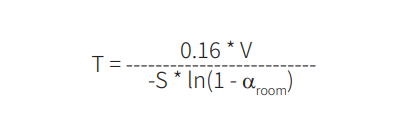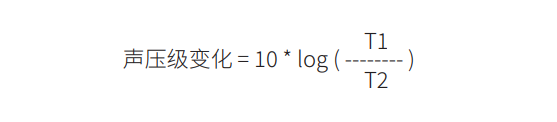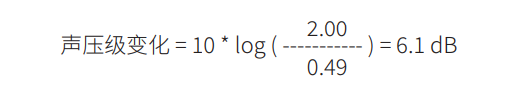硬核科普：混响时间，赛宾公式和伊林公式
混响时间可以说是声学工程师们最熟悉的词之一，通过添加或减少吸声材料（如布艺沙发，地毯，声学画或特殊的天花板涂层等）的方式就可以控制混响时间的大小，从而“操纵”一个地方的声品质。
测量混响时间，从最简单的“拍拍手”，到使用专业声学仪器，测量精度也不断提高。但工程中从前期设计到后期施工，每个环节都进行实地测量几乎是不现实的，所以仿真软件成为一大利器，混响时间仿真的基础，就是今天要介绍的赛宾公式和伊林公式。
后期实践中人们发展出了更多混响时间计算公式，但赛宾和伊林是最经典的。
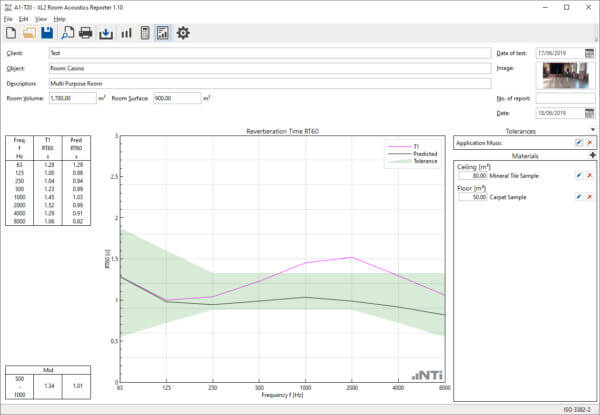
室内声学报告软件可以进行混响时间模拟计算
标准的软件模拟过程使用了赛宾公式，依据 DIN EN 12354-6: 2004 标准。赛宾公式由物理学家 Wallace Clement Sabine（1868-1919）提出。
赛宾公式
1895年，哈佛大学 Fogg 艺术博物馆落成，但是发现博物馆的礼堂音质模糊不清。当时哈佛大学物理系最年轻的助理教授赛宾被请来解决这个问题。当时赛宾依靠耳朵作为接收器，并用一个停表作为计时器，大量的坐垫作为吸声材料，研究吸声量 A与混响时间 RT 的关系。在 1900 年赛宾发表著名论文《混响》，提出了混响时间这一概念，并得出计算混响时间的公式 - 赛宾公式。自此奠定了厅堂声学甚至是整个建筑声学的科学基础。混响时间至今仍是厅堂音质评价首选的物理指标。
直接看公式：
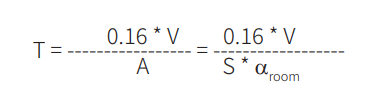
这里为简化计算，空气的声吸收和室内物品导致的容积变化不在考虑范围内。根据 DIN EN 12354-6: 2004 标准，假设声速为 345.6 m/s，所以直接采用赛宾公式内的系数 0.16。
不要被吓到，这个“唬人”的公式本身并不复杂，这里：
- T ... 混响时间 [s]
- V ... 房间净容积 [m3]
- A ... 总的或能量等效吸声量 [m2]
- S ... 地板，墙壁和天花板总面积 [m2]
- αroom ... 平均吸声系数，无单位
各厂家一般都会标注自己产品在各频率的吸声系数
仿真软件模拟处在室内的吸声材料，试件和人等的吸声效果。让你直观了解声学性能改变情况，以期达到标准要求。
通过以下公式分析吸声体的影响：
这个公式也只是看起来吓人，其中
- S ... 地板，墙壁和天花板总面积 [m2]
- αroom ... 平均吸声系数，无单位
- αi ... 吸声体 i 的吸声系数，无单位
- Aobjj ... 物体 j 的吸声量 [m2]
看，只要代入数据，灵活使用以上两个公式进行简单的乘除运算，我们自己也能“仿真”。
混响时间减小，室内声压级也会变小。
限制
实践中，赛宾公式常用来优化室内声学性能。该公式基于以下假设：
- 空间声场为扩散场（混响场）；*
- 室内的吸声面均匀分布（某些情况下，不同位置吸声系数最大能偏差 3）；
- 鞋盒状规则空间，最大尺寸比 1: 5；
- 室内没有太多物品，它们最多只能占容积的 20%.
如果无法满足上述条件，实际混响时间将大于模拟值。
* 声音能量均匀，直达声和反射声混在一起，在各个方向无规则分布，这样的声场就是扩散场或混响场。相对应的是自由场，也就是声音发出去就不回来的声场，消声室就是人造的自由场。还有一种叫压力场，这里声音波长比其所在空间的尺寸还大，声音分布均匀，人耳带着耳机就形成了简单的压力场。
消声室是最重要的声学室之一，此外还有混响室，隔音室，声学风洞等各类声学实验室。
不懂没关系，来做例题啊。
范例 1 某长方体房间长 8 m，宽 7 m，高 3 m。其地板面积 56 m2，总面积 202 m2，容积 168 m3。测得 1 kHz 的混响时间是 2 秒。则房间吸声系数：
接着将天花板上的 56 m2 区域更换为 0.8 吸声系数的材料：
范例 2 接范例 1：一般情况下，天花板，墙壁和地板的吸声系数是不同的，要精确模拟，还应减去原始天花板的声吸收，假设原水泥天花板吸声系数为 0.03：
伊林（Eyring）公式
Carl Ferdinand Eyring，墨西哥裔声物理学家
对于平均吸声系数大于 0.25（4 kHz 下大于 0.2）的应用，赛宾公式会得出过高的混响时间。因此，在赛宾公式的基础上，人们又进行了大量的研究，作出了一些修正，得出了在工程界普遍应用的伊林公式（或伊林 - 努特生公式）。
它能在这种情况下计算出更具代表性的混响时间。
其中
- T ... 混响时间 [s]
- V ... 房间净容积 [m3]
- S ... 地板，墙壁和天花板总面积 [m2]
- αroom ... 平均吸声系数，无单位
混响时间对声压级的影响
混响时间减小，房间将变得更加安静 - 因为直达声不受影响，而来自房间边界等各处的反射声变小了 - 总声压级减小。我们同样可以计算声压级的变化。使用的公式如下：
其中
- T1 ... 实际混响时间 [s]
- T2 ... 预估混响时间 [s]
范例 3 根据范例 1 中的计算结果，声压级将变化：
测量混响时间
无论如何，软件仿的再真终究是仿，考察混响时间的客观方法还是测量。实践中一般通过测量 RT60 评估混响时间。
标准中列出了一些典型场所和推荐的 RT60 值：
| 场所 | 体积 | 临界距离 Dc | 推荐 RT60 |
| 录音棚 | < 50 m3 | 1.5 m | 0.3 s |
| 教室 | < 200 m3 | 2 m | 0.4 - 0.6 s |
| 办公室 | < 1'000 m3 | 3.5 m | 0.5 - 1.1 s |
| 报告厅 | < 5'000 m3 | 6 m | 1.0 - 1.5 s |
| 音乐厅，剧院 | < 20'000 m3 | 11 m | 1.4 - 2.0 s |
| 教堂 | 2 - 10 s |